Солнце, луна, древние праздники и новомодные теории

СОЛНЦЕ, ЛУНА, ДРЕВНИЕ ПРАЗДНИКИ И НОВОМОДНЫЕ ТЕОРИИ.

(с) Красильников 1999

Когда будет пасха в 2000 году?

Спросите кого-нибудь - когда в будущем году будет рождество? Ваш собеседник сильно удивится - конечно, 7-го января, как и в этом, и в прошлом году. А теперь поинтересуйтесь - а когда будет пасха? Большинство людей этот вопрос поставит в тупик. Действительно, ряд церковных праздников (в том числе и главный христианский праздник - пасха) - переходящие, т.е. в разные годы они приходятся на разные даты календаря.

Тем не менее ответить на этот вопрос не так уж и сложно. Сперва надо найти остаток от деления номера года на 19 - обозначим его через c. Затем на основании этого остатка нужно определить "опорную дату" из таблицы 1. Даты в этой таблице даны по старому стилю (юлианскому календарю), и для перехода к григорианскому календарю надо к полученной дате прибавить 13 дней (для годов в XX и XXI веке). Пасха будет в ближайшее воскресенье строго после найденной нами даты. (Слова "строго после" означают, что если наша дата пришлась на воскресенье, то пасха будет через неделю после нее - в следующее воскресенье).

Таблица 1. Опорные даты для определения даты пасхи. c - остаток от деления номера года на 19, d - количество дней от 21 марта до опорной даты.

cОпорная дата d 05 апреля 15 125 марта 4 213 апреля23 32 апреля 12 422 марта 1 510 апреля20 630 марта 9 718 апреля28 87 апреля 17 927 марта 61015 апреля25114 апреля 141224 марта 21312 апреля22141 апреля 111521 марта 0169 апреля 191729 марта 81817 апреля27

Для примера определим даты пасхи в 1999 и 2000 году. Разделим 1999 на 19 и получим в остатке 4. Опорная дата из таблицы - 22 марта. Прибавим 13 дней: 22+13=35. Так как в марте всего 31 день, вычтем 31 из полученного результата: 35-31=4, т.е. 4-е апреля по новому стилю. Поскольку 4-е апреля в этом году пришлось на воскресенье, то пасха праздновалась неделю спустя - 11 апреля.

При делении 2000 на 19 получаем остаток 5 и опорную дату 10 апреля по старому и 23 - по новому стилю. 23 апреля в 2000 году тоже приходится на воскресенье, поэтому пасха будет праздноваться неделю спустя - 30 апреля.

Таким образом, вопрос "когда была (будет) пасха в N-ом году?" не столь труден, как может показаться: для ответа на него нужно всего лишь уметь находить остаток от деления N на 19 и иметь две таблицы, одна из которых приведена выше, а вторая - табель-календарь на интересующий нас год.

А как обойтись без таблиц?

Если нас интересует не текущий год, то, как правило, табель-календаря у нас под рукой не окажется. Хотелось бы уметь при расчетах даты пасхи обходиться без вспомогательных таблиц. Оказывается, это тоже не очень сложно. Для начала заметим, что таблица 1 имеет достаточно регулярное строение: при переходе к следующему году дата сдвигается либо на 11 дней раньше, либо - если при сдвиге получается дата до 21 марта - на 19 дней позже. Вследствие этого числа d из последнего столбца таблицы 1 (количество дней, прошедших от 21 марта до опорной даты) описываются простым выражением d=(19*с+15)%30 (знак процента используется здесь и далее для обозначения остатка от деления). Поэтому без приведенной выше таблицы обойтись очень легко. Можно также обходиться и без табель-календаря: единственное, для чего он нам нужен - это узнать, на какой день недели приходится полученная нами опорная дата, чтобы найти следующее за ней воскресенье. Но это можно определить и непосредственно по номеру года. Не вдаваясь в дальнейшие подробности, приведем полный алгоритм для определения даты пасхи для произвольного года, заимствованный из [2].

Зададим целое число year - номер интересующего нас года. Затем последовательно вычислим

a = year % 4;
b = year % 7;
c = year % 19;
d = ( 19 * c + 15 ) % 30;
e = ( 2 * a + 4 * b - d + 34 ) % 7;
f = 3 + (d + e + 21) / 31;
g = ( d + e + 21 ) % 31;
month = f;
day = g + 1;

В результате переменные month и day получат значения месяца и дня пасхи для интересующего нас года.

Все операции деления в этом алгоритме - целочисленные, т.е. дающие в результате целую часть частного. Знак процента обозначает операцию нахождения остатка от деления.

(Некоторые комментарии. Переменная d - это сдвиг опорной даты от 21 марта, переменная е - календарная поправка, значение которой равно 0, если опорная дата приходится на субботу, 1 - на пятницу, 2 - на четверг, :, 6 - на воскресенье, т.е. уменьшенное на единицу число дней между опорной датой и следующим за ней воскресеньем).

Следует иметь в виду, что данный алгоритм выдает дату по старому стилю (юлианскому календарю), т.е. ее нужно перевести в новый стиль. Для XX и XXI веков этот перевод состоит в прибавлении 13 дней к полученной дате.

Заметим, что в приведенном алгоритме вначале находятся остатки от деления номера года на 4, 7 и 19, а в дальнейших вычислениях используются только эти остатки. Из этого следует, что результаты вычислений будут повторяться с периодом, равным произведению трех делителей (т.к. эти делители взаимно просты). Произведение 4*7*19 равно 532. Поэтому спустя 532 года пасха происходит в ту же самую дату (разумеется, по юлианскому календарю). Этот период в 532 года в теории пасхальных вычислений называется великим индиктионом. Отметим также, что увеличенное на единицу значение c из таблицы 1 (т.е. для ее первой строки - 1, для второй - 2 и т.д.) называется золотым числом.

Следует сказать, что в действительности пасхальные вычисления были существенно более сложными. В них использовались такие специфические понятия, как "эпакты", "вруцелетные буквы" и т.п. и составлялся ряд вспомогательных таблиц. Изложенное выше - это до предела упрощенная их суть. Мы не будем вдаваться в подробности исходной методики расчета пасхальных дат - это чрезмерно увеличило бы объем данной статьи. Интересующийся читатель может самостоятельно найти эти подробности в литературе, например, в работе И.А.Климишина [1].

А при чем тут Луна?

Теперь мы умеем вычислять даты пасхи, но смысл этих вычислений остается малопонятным. Чтобы понять его, следует вспомнить, что пасхальное воскресенье - это первое воскресенье после так называемого пасхального полнолуния, т.е. первого полнолуния, которое происходит в день весеннего равноденствия или после него. Теперь нам ясно, что описанные ранее вычисления предполагают, что весеннее равноденствие происходит 21 марта (т.к. самая ранняя из дат в таблице 1 - 21 марта), а загадочная "опорная дата" - это дата пасхального полнолуния в этом году.

Проверим нашу догадку. Мы уже вычислили, что в 1999 году расчетная дата пасхального полнолуния - 4 апреля по новому стилю. Определим с помощью какого-нибудь календаря, где указаны фазы Луны, когда было полнолуние в начале апреля. Оказывается, ближайшее к найденной нами дате полнолуние произошло вечером 31 марта. Концы с концами у нас не сошлись - налицо расхождение в четверо суток. Отчего это произошло?

Посмотрим еще раз на методику вычисления даты пасхального полнолуния. Она очень проста - составлено "расписание дат полнолуний" (см. таблицу 1), которое повторяется через 19 лет, т.е. предполагается, что через 19 лет полнолуние придется на ту же самую дату юлианского календаря. Этот факт известен астрономам уже свыше двух тысяч лет и носит название "Метонова цикла". Он основан на том, что 19 лет почти точно равны 235 лунным месяцам. Действительно, средняя продолжительность года в юлианском календаре - 365.25 дней, а продолжительность лунного (синодического) месяца - 29.530588 дней. 365.25*19=6939,75 дней, а 29.530588*235=6939,68818 дней. Эти два числа действительно очень близки: их разность равна 0,06182 суток, или 1.48 часа. Итак, 235 лунных месяцев короче девятнадцати лет юлианского календаря всего лишь на полтора часа. Следовательно, если в неком году полнолуние произошло, например, 25 марта в 20 часов, то через 19 лет оно произойдет тоже 25 марта, но на полтора часа раньше, т.е. в 18 часов 30 минут.

Следует заметить, что утверждение "через 19 лет полнолуние произойдет в ту же самую дату, но на полтора часа раньше" верно лишь в среднем - по двум причинам. Во-первых, 19 лет юлианского календаря могут содержать лишь целое число суток - 6939 или 6940 в зависимости от того, содержат ли эти 19 лет 4 или 5 високосных. С другой стороны, 235 лунных месяцев всегда содержат примерно 6939,688 суток, поэтому через 19 лет момент полнолуния будет либо на 0.688 суток позже, либо на 0.312 суток раньше - в зависимости от количества високосных лет в конкретном 19-летнем интервале.

Во-вторых, приведенная выше продолжительность синодического месяца - 29.530588 суток - это опять-таки средняя продолжительность, моменты же истинных полнолуний из-за неравномерного движения Луны по орбите могут опережать моменты средних полнолуний (условных полнолуний, происходящих ровно через указанный интервал времени, как если бы движение Луны по орбите было строго равномерным) или отставать от них.

На рисунке 1 показано расхождение моментов средних и истинных полнолуний в 1980-2000 гг. Как ясно из графика, максимальное расхождение составляет несколько более полусуток.

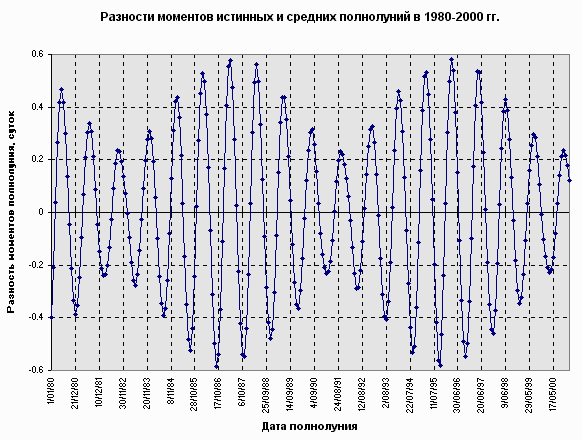
Рисунок 1. Разность моментов истинных и средних полнолуний в 1980-2000 гг.

Однако в среднем на протяжении больших интервалов времени эта закономерность - сдвиг моментов полнолуний на полтора часа за 19 лет - выполняется достаточно точно.

На первый взгляд кажется, что полтора часа за 19 лет - достаточно малая величина. Однако это не так. Действительно, если за 19 лет набегает разница в 0.062 суток, то расхождение на целые сутки накопится за 1/0.062=16.13 19-летних циклов, или примерно за 306 лет.

Для 1999 года мы имеем расхождение между расчетным и истинным пасхальным полнолунием около 4 суток. На основании этого можно сделать оценку эпохи (очень грубую!), в которую было составлено расписание пасхальных полнолуний. Так как расхождение за сутки накапливается за 300 с небольшим лет, то эпоха, когда расчетное и астрономическое полнолуния совпадали, была более тысячи лет назад.

Когда это было?

Попытаемся провести более тщательное исследование вопроса о времени составления правил определения даты пасхи. Вообще говоря, в этих правилах имеются целых две возможности для их датировки. Во-первых, как мы видели, в методике расчета предполагается, что весеннее равноденствие приходится на 21 марта по старому стилю. Хорошо известно, что из-за расхождения между длиной тропического года (365.2422 суток) и средней длиной года в юлианском календаре (365.25 суток) дата весеннего равноденствия смещается на сутки за 128 лет.

Рисунок 2. Моменты весенних равноденствий в 200-600 гг. н.э.

На рисунке 2 показаны моменты весеннего равноденствия в 200-600 гг. н.э. Даты даны по старому стилю, время - мировое (гринвичское). (Строгости ради надо заметить, что в Константинополе - центре восточного христианства в древности - местное время опережает мировое почти на два часа, но мы пренебрежем этой разницей).

Моменты равноденствий, как и большинство расчетов в данной статье, были выполнены по формулам, приведенным в книге Ж.Мееса "Астрономические формулы для калькуляторов" [2].

Из рисунка ясно, что весеннее равноденствие происходило 21 марта в начале III века н.э - за век до Никейского собора, на котором были выработаны правила празднования пасхи (325 г.).

На врезке в правом верхнем углу рисунка 2 показан крупным планом участок графика для 300-340 гг. На нем четко видно, как "работает" юлианский календарь. Так как тропический год (интервал между равноденствиями) почти на четверть суток больше длины простого года в 365 суток, то момент весеннего равноденствия в простом году наступает почти на 6 часов позже, чем в предыдущем. На протяжении трех простых лет момент равноденствия смещается почти на 18 часов. Каждый четвертый год в календаре - високосный (с добавленным дополнительным днем), и в нем момент равноденствия наступает ранее, чем в предыдущем, чуть более чем на 18 часов. Таким образом, високосный год компенсирует ошибку, накопившуюся за три простых года. Но компенсация эта - с небольшим избытком, примерно в 45 минут, и моменты равноденствий плавно смещаются на все более ранние даты календаря. За 32 четырехлетних цикла (т.е. за 128 лет) накапливается ошибка в сутки.

Попутно обсудим вопрос о методике, с которой могли определять момент равноденствия в древности, и ее точности. В известном труде Птолемея "Альмагест" описан простой и остроумный прибор, применявшийся для этой цели предшественниками Птолемея и им самим - экваториальное кольцо. Это - металлическое кольцо, установленное так, что его плоскость совпадает с плоскостью небесного экватора. Иными словами, южная часть плоскости кольца должна быть отклонена от вертикали на угол, равный широте места наблюдений. В момент равноденствия Солнце находится на небесном экваторе, и тень от верхней части кольца падает точно на нижнюю, при этом освещаются одновременно верхний и нижний края затененной части. Таким образом, момент равноденствия наблюдается непосредственно.

Рисунок 3. Экваториальное кольцо и принцип его действия (справа). Сверху вниз: Солнце севернее небесного экватора, освещен верхний край кольца; Солнце точно на экваторе, тень падает точно на кольцо; Солнце южнее экватора, освещен нижний край кольца.

Экваториальное кольцо позволяет достаточно точно определить момент равноденствия. Согласно приведенным в труде Птолемея "Альмагест" [3] данным, с помощью этого прибора Гиппарх во II веке до н.э. провел такие определения на протяжении ряда лет. Современные расчеты показывают, что для большинства наблюдений ошибка составляла примерно четверть суток и не превышала 10 часов в самом худшем случае. У самого Птолемея ошибка определения момента весеннего равноденствия была существенно больше - около 20 часов.

Если предположить, что ошибка в определении моментов весеннего равноденствия у составителей правил расчета даты пасхи была вдвое больше соответствующей ошибки у Птолемея (т.е. около двух суток), то мы получим, что эти правила были составлены во II-V веках н.э.

Второй метод определения времени составления методики расчета даты пасхи - это определение той эпохи, когда получаемые на основе этой методики расчетные даты полнолуний совпадают с фактическими.

Задача эта не так проста, как может показаться на первый взгляд. Сначала выясним, как в древности определялась дата полнолуния. Свет на это проливает встречающееся в церковных документах название полнолуния - "14-я Луна". "Первой Луной" считалась так называемая неомения. Это греческое слово означает "новолуние", но имеет несколько иной смысл. Сейчас под новолунием подразумевается момент соединения Луны и Солнца. Неомения же - это первое появление лунного серпа на вечернем небе (после новолуния в современном смысле). День неомении считался первым днем, а под полнолунием понимался 14-й - т.е. 13 суток спустя.

Как утверждается в книге И.А.Климишина "Календарь и хронология" [1], на широте 32.5 градусов (это широта древнего Вавилона) Луну весной на закате нельзя наблюдать ранее чем через 16 часов 30 минут после новолуния, а на широте 38 градусов (широта Афин, южной Италии и Малой Азии) - ранее чем через 23 часа. Следовательно, дата неомении существенно зависит от места наблюдения - если, допустим, возраст Луны (время от момента новолуния) на закате составляет 20 часов, то в северной Африке Луна на закате будет видна, а в Италии - нет; там неомению будут наблюдать лишь сутки спустя. По причинам, которые станут ясны ниже, мы будем проводить расчеты, предполагая, что наблюдения неомении происходили в Александрии. Широта Александрии - 31 градус 13 минут, а местное время опережает мировое на 2 часа. Будем считать, что неомения наблюдается, если возраст Луны на закате составляет от 0.7 до 1.7 суток. 13 суток спустя возраст Луны составит от 13.7 до 14.7 суток.

Проведем расчет истинного возраста Луны (т.е. промежутка времени от истинного новолуния) на 18 часов всемирного (гринвичского) времени расчетного пасхального полнолуния, даваемого правилами расчета пасхи. Результаты расчета представлены на рисунке 4. Как ясно из вышеизложенного, если возраст Луны вечером расчетного пасхального полнолуния находится в пределах от 13.7 до 14.7 суток (это равносильно тому, что в день неомении возраст Луны находится в пределах от 0.7 до 1.7 суток), то расчетное полнолуние совпадает с установленным из прямых наблюдений "днем 14-й Луны". Здесь нам надо учесть разность мирового времени и местного времени Александрии. Когда в Александрии 18 часов (закат вблизи равноденствия), то по мировому времени в этот момент всего 16 часов - т.е. на 2/24 суток менее. Наши же расчеты возраста Луны выполнены на 18 часов мирового времени - следовательно, диапазон возраста надо уменьшить примерно на 0.1 суток - т.е. интервал возраста Луны на 18 часов мирового времени должен составлять примерно от 13.6 до 14.6 суток. Среднее значение возраста Луны составляет, очевидно, 14.1 суток. Итак, если возраст Луны превышает 14.6 суток, например, находится в пределах от 14.6 до 15.6 суток, то неомения должна была наблюдаться сутками ранее и расчетное полнолуние на сутки запаздывает относительно истинного, и т.д. Если наблюдения неомении проводятся в другом месте, то указанный интервал допустимого возраста Луны изменяется. Так, для Рима минимальный интервал между новолунием и неоменией - примерно сутки (Рим несколько севернее широты 38 градусов, для которой, согласно Климишину, он составляет 23 часа). Местное время там запаздывает относительно мирового менее чем на час. Если пренебречь этим запаздыванием (менее 0.05 суток), то для Рима интервал допустимого возраста Луны составляет от 14 до 15 часов. Таким образом, зависимость даты неомении от географического положения наблюдателя довольно ощутима. Разность допустимого возраста Луны для Александрии и Рима составляет 0.4 суток - это значит, что в 40% случаев наблюдатель в Риме будет фиксировать неомению на сутки позже наблюдателя в Александрии.

Рисунок 4. Истинный возраст Луны на 18 часов в расчетное пасхальное полнолуние (по мировому времени) в 200-900 гг.н.э.

Прежде всего отметим, что использованный для расчета дат полнолуний метонов цикл не слишком-то точен. На графике постоянно встречаются выбросы вверх и вниз от среднего значения (желтая линия) величиной до полутора суток. Это означает, что описанная выше методика принципиально не может быть точной - даваемые ей даты полнолуний в значительной части случаев неизбежно будут опережать устанавливаемые по наблюдениям даты "четырнадцатой Луны" на сутки или отставать от них на сутки. Далее заметим, что средний возраст Луны монотонно возрастает на сутки за 300 с небольшим лет. Среднее значение в 14.1 суток достигается в первой половине V века.

Эти же даные представлены в таблице 2. Для каждого 19-летнего промежутка, используемого при расчете пасхальных дат, в интервале 323-701 гг., дано количество лет, для которых устанавливаемая из наблюдений дата "14-й Луны" совпадает с расчетной датой пасхального полнолуния, опережает ее или запаздывает. Будем считать, что если возраст Луны на 18 часов всемирного времени лежит в пределах 13.6 - 14.6 суток, то расчетное полнолуние (для наблюдателя в Александрии) совпадает с "днем 14-й Луны", если же он находится в пределах 12.6 - 13.6 суток, то расчетное полнолуние опережает наблюдаемое на сутки, для интервала 14.6 - 15.6 суток имеет место запаздывание на сутки и т.д.

Таблица 2. Совпадение наблюдаемых дат "14-й Луны" и расчетных дат пасхальных полнолуний в 209-911 гг.

Интервал летРанее на двое суток Ранее на сутки Совпадает Позже на сутки Позже на двое суток Позже на трое суток 209-227 012 7 0 0 0228-246 111 6 1 0 0247-265 1 9 9 0 0 0266-284 2 611 0 0 0285-303 011 8 0 0 0304-322 0 811 0 0 0323-341 1 511 2 0 0342-360 0 810 1 0 0361-379 0 7 9 3 0 0380-398 0 611 2 0 0399-417 0 413 2 0 0418-436 0 511 3 0 0437-455 0 215 2 0 0456-474 0 212 5 0 0475-493 0 311 5 0 0494-512 0 111 7 0 0513-531 0 210 7 0 0532-550 0 012 7 0 0551-569 0 1 9 9 0 0570-588 0 012 6 1 0589-607 0 0 910 0 0608-626 0 1 611 1 0627-645 0 0 811 0 0646-664 0 1 512 1 0665-683 0 0 712 0 0684-702 0 0 415 0 0703-721 0 0 510 4 0722-740 0 0 610 3 0741-759 0 0 313 3 0760-778 0 0 412 3 0779-797 0 0 213 4 0798-816 0 0 311 5 0817-835 0 0 114 4 0836-854 0 0 110 8 0855-873 0 0 111 6 1874-892 0 0 1 9 8 1893-911 0 0 2 611 0

Из таблицы также видно, что наилучшее совпадение между наблюдаемыми и расчетными пасхальными полнолуниями имело место в первой половине V века - в это время расчетная дата полнолуния совпадала с наблюдаемым "днем 14-й Луны" в подавляющем большинстве случаев, а число опережений и запаздываний было примерно одинаковым.

Поставим вопрос - с какой точностью мы можем датировать составление "расписания полнолуний", используемого при расчете дат пасхи? Вспомним, как составлена таблица 1 - для каждого следующего года дата полнолуния сдвигается на 11 дней ранее или на 19 дней позже. Это - обычный способ составления таблиц фаз Луны в средние века. (Кстати, для последнего года в таблице дана дата 17 апреля. Если попытаться "замкнуть цикл" и перейти от последней строки таблицы к первой, вычтя 11 дней, то мы получим 6 апреля, а в первой строке таблицы дана дата 5 апреля - т.е. цикл не замыкается. Это обстоятельство было предметом недоумений в средние века и называлось "скачком Луны": "Луна совершает скачок в 1 день каждые 19 лет").

Именно такая регулярная структура таблицы 1 позволяет описать ее простым выражением d=(19*с+15)%30.

Очевидно, что минимальный интервал времени, на который мы можем передвинуть расписание полнолуний для его лучшего соответствия с реальными "днями 14-й Луны" - это одни сутки. Из этого следует, что если расписание составлялось, например, в 304-322 гг., (из таблицы 2 видно, что для этого времени в 8 случаях наблюдалось опережение расчетного полнолуния на сутки, а в 11 случаях - совпадение), то у его составителей был бы выбор из двух возможностей. Первая возможность - принять рассмотренное выше расписание. Вторая - сдвинуть расписание полнолуний на сутки вперед, тогда наблюдалось бы совпадение дат в 8 случаях и запаздывание расчетного полнолуния на сутки - в 11 случаях). И та и другая возможность дает большое количество расхождений дат, но первая из них более удовлетворительна - совпадение имеет место в более чем половине случаев. Очевидно, точность нашей датировки - примерно плюс-минус 200 лет (т.е. несколько более времени смещения возраста Луны на полсуток) от времени наилучшего соответствия расписания полнолуний реальным "дням 14-й Луны" (т.е. первой половины V века), т.к. вне этого интервала сдвинутое на сутки расписание полнолуний лучше соответствует наблюдениям, чем расписание, зафиксированное в таблице 1.

Итак, приведенное в таблице 1 расписание полнолуний было скорее всего составлено примерно между 250 и 600 гг. Из таблицы 2 можно заключить, что именно в этот период наблюдаемые полнолуния совпадали с расчетными более чем в половине случаев. Разумеется, этот вывод справедлив, если при составлении расписания действительно проводились регулярные наблюдения неомений в течение ряда лет с целью добиться наилучшего согласования между расчетными и наблюдаемыми полнолуниями. Если же расписание полнолуний устанавливалось на основе малого количества наблюдений, то интервал датировки следует существенно увеличить, т.к. в качестве опорных наблюдений могли быть использованы "выбросы", сильно отклоняющиеся от среднего времени полнолуния. Кроме того, на наблюдение неомении сильно влияют атмосферные условия - если они неблагоприятны, то первое появление лунного серпа на вечернем небе легко пропустить. Напомним также, что расчет выполнялся в предположении, что наблюдения неомений проводились в Александрии. Для более северных широт наблюдаемые полнолуния будут происходить несколько позже. В первоначальном варианте данной работы предполагалось совпадение истинного и расчетного полнолуния при возрасте Луны от 14 до 15 суток (это справедливо для наблюдателя, находящегося, например, в Риме). Поскольку интервал допустимого возраста Луны в этом случае позже на 0.4 суток, то интервал датировки получился сдвинутым приблизительно на 300*0.4=120 лет позже, т.е. примерно с 370 по 720 гг.

А что говорит история?

В книге И.А.Климишина [1] достаточно подробно освещена история выработки правил пасхальных вычислений. Интересующихся этим вопросом более подробно отошлем к указанной работе (стр. 209-214), здесь же кратко скажем, что во времена до и даже после Никейского собора среди христиан имелись очень существенные расзногласия о дате празднования пасхи. Некоторые секты отмечали пасху вместе с евреями, в ночь с 14 по 15 нисана по еврейскому календарю. Александрийские и сирийские христиане пользовались методиками вычисления пасхального полнолуния на основании 19-летнего цикла и отмечали пасху в следующее за ним воскресенье, хотя "расписания полнолуний" (так называемые "александрийский" и "сирийский" циклы), а следовательно, и даты пасхи, у них различались. Христиане в Риме использовали для расчета пасхальных полнолуний 84-летний цикл. Наконец, одна из сект отмечала пасху в фиксированную календарную дату - 25 марта.

Одним из двух главных пунктов "повестки дня" на Никейском соборе (325 г. н.э.) и был вопрос о правилах празднования пасхи. О том, что именно было решено на соборе, сегодня известно очень мало - текста постановления собора не было в церковных архивах уже в начале V века. Сохранилось лишь послание императора Константина епископам, не присутствовавшим на соборе. В нем Константин высказывает лишь общие пожелания: "...На том же Соборе было исследование и касательно святейшого дня Пасхи, и общим мнением признано за благо - всем и везде праздновать ее в один и тот же день; ибо, что может быть прекраснее и благоговейнее, когда праздник, дарующий нам надежду бессмертия, неизменно совершается всеми по одному чину и известным образом? Прежде всего показалось неприличным праздновать тот святейший праздник по обыкновению иудеев... Отвергнув их обыкновение, гораздо лучше будет тем же истинным порядком, который мы соблюдали с самого первого дня страстей до настоящего времени, образ этого празднования продолжить и в будущем. Итак, пусть не будет у нас ничего общего с народом иудейским, потому что нам указан Спасителем другой путь...Вступая на него единомысленно, возлюбленные братья, отделимся от того постыдного общества, ибо поистине странно самохвальство иудеев, будто, независимо от их постановления, мы не можем соблюдать этого... [Иудеи,] находясь в заблуждении и стоя весьма далеко от надлежащего исправления, в одном и том же году празднуют Пасху в другой раз... Мы, конечно, не потерпим, чтобы наша Пасха была празднуема в одном и том же году в другой раз. А если сказанного недостаточно, то ваше благоразумие само должно всячески заботиться и желать, чтобы чистые ваши души ни в чем не сообщались и не сходились с обычаями людей самых негодных... Да размыслит благоразумие вашего преподобия, как худо и неприлично то, что в известное время одни соблюдают пост, а другие совершают пиры, и что после дней Пасхи одни проводят время в празднованиях и покое, а другие держат положенные посты... Когда же все это надлежало исправить так, чтобы у нас не оставалось ничего общего с господоубийцами и отцеубийцами, и когда порядок, которому в этом отношении следуют все Церкви западных, южных, северных и некоторых восточных областей империи, действительно благоприличен, а потому в настоящее время всеми признан единым, то ручаюсь, что он понравится и вашему благоразумию: ваша рассудительность, конечно, с удовольствием примет то, что единомысленно и согласно соблюдается в Риме и Африке, во всей Италии, Египте, Испании, Галлии, Британии, Ливии, в целой Греции, в областях азийской, понтийской и киликийской; она разочтет, что в поименованных местах не только большее число Церквей, но и что все желают этого порядка, как самого лучшего. Да, кажется, и здравый смысл требует, чтобы мы не имели никакого общения с клятвопреступными иудеями. Короче говоря: по общему суду всех, постановлено святейший праздник Пасхи совершать в один и тот же день." [5, c.28-30 (часть 1, глава 9)]. Конкретные же правила определения пасхальных дат в послании отсутствуют.

Скорее всего, собор сформулировал некие общие правила, которым должна удовлетворять дата пасхи, конкретная же вычислительная схема, которую западные христиане использовали свыше тысячи лет, а православные применяют до сих пор, была выработана несколько позже. На стр. 87 книги Климишина [1] явно сказано: "Уже в V веке н.э. было составлено расписание новолуний на 19-летний лунный цикл, которое и используется неизменно до сих пор при определении фаз Луны". Действительно, из представленных выше данных расчетов (рисунок 4 и таблица 2) следует, что как раз в V веке реальным полнолуниям лучше всего соответствовало именно приведенное в таблице 1 расписание полнолуний - при сдвиге его на сутки вперед в большей части случаев наблюдалось бы отставание расчетных полнолуний от реальных. В другом месте Климишин утверждает, что "Таблицы пасхальных полнолуний были составлены в IV-VI вв., на их основании и проводились дальнейшие расчеты" [1, стр. 215]. Таким образом, методика вычислений даты пасхального полнолуния, видимо, складывалась в течение значительного времени после Никейского собора.

В подтверждение этой точки зрения И.А.Климишин приводит также высказывание профессора Ленинградской духовной академии Л.Воронова: "...Никейский собор... не ввел во всеобщее, непременное и вечное употребление какую-либо строго определенную пасхалию как как унифицированную систему расчетов и определения дня празднования Пасхи", поскольку "сама александрийская пасхалия вряд ли мыслилась как "вечная и неисходная"". [1, стр. 226]

Тем не менее возможно, что известное нам сегодня расписание полнолуний зафиксировано уже во время Никейского собора. Как видно из таблицы 2, начиная с IV века именно оно обеспечивает лучшее совпадение расчетных и наблюдаемых полнолуний, чем сдвинутое на сутки.

Теперь следует пояснить, почему расчет дат наблюдаемых полнолуний выполнялся нами в предположении, что наблюдатель находится в Александрии. На Никейском соборе за основу была принята александрийская традиция, и дату празднования Пасхи в первые годы после собора устанавливал Патриарх Александрийский. "Решение по поводу Пасхи явилось успехом александрийской партии. Обычай празднования Пасхи в первое воскресенье вслед за весенним полнолунием был обычаем александрийского происхождения, тогда как большинство христиан Востока придерживалось иудейской традиции" [5, с. 329].

Интересно, что уже много веков точно неизвестно, кем и когда было составлено это расписание полнолуний. Получается, что все христиане почти тысячу лет использовали для вычисления даты пасхи расчетные правила неизвестного происхождения, непонятно когда выработанные и, возможно, не канонизированные официально, а ставшие "стандартом де-факто".

Надо отметить, что в книге Климишина [1] имеются и другие высказывания, на первый взгляд противоречащие недавно приведенной цитате. Например, на стр. 214 говорится буквально следующее: "B III в. caмa мeтoдикa pacчeтa дaт пacxи yжe былa нaдeжнo paзpaбoтaнa." Однако из вышеприведенного анализа ясно, что речь здесь идет именно о методике, т.е. использовании 19-летнего лунного цикла для определения дат полнолуний - и ниоткуда не следует, что конкретное расписание полнолуний, используемое православной церковью по сей день, было также составлено в III веке...

Обратим также внимание на следующий примечательный факт. Как мы уже знаем, период в 532 года, с которым повторяются даты пасхи, называется великим индиктионом. Из литературы известно, что великие индиктионы начинались в 345, 877, 1409 и 1941 гг. Если найти остаток от деления номера первого года какого-нибудь из великих индиктионов (например, 345) на 19, то мы получим 3. Иными словами, 19-летний период, положенный в основу вычисления даты пасхи, начинается на три года раньше великого индиктиона. Это расхождение - лишнее свидетельство долгой истории развития вычислений даты пасхи. Вначале эти вычисления выполнялись на основе так называемых круга Луны - номера года в 19-летнем цикле и круга Солнца - номера года в 28-летнем цикле. Круг Луны можно найти как остаток от деления уменьшенного на 2 номера года по нашему летоисчислению на 19. Круг Солнца находится как остаток от деления уменьшенного на 8 номера года на 28. (Если соответствующий остаток равен нулю, то круг Луны равен 19, а круг Солнца - 28). Найдем круг Луны и круг Солнца для 345 года: (345-2)%19 = 1, (345-8)%28 = 1, т.е. начало великих индиктионов совпадает с первым годом круга Солнца и круга Луны. Позже вычисления даты пасхи стали выполняться на основе золотого числа. Это - также номер года в 19-летнем цикле, но начало этого цикла смещено относительно "круга Луны" на 3 года. Отсчет же великих индиктионов остался прежним. (То, что известное нам расписание полнолуний составлено на основе "золотого числа", а не "круга Луны", подтверждается тем, что "скачок Луны" - уменьшенный на сутки интервал между полнолуниями в двух соседних годах, - "спрятан" в последней строке таблицы и явно в ней не присутствует; он проявляется лишь при продолжении этой таблицы на следующий девятнадцатилетний период.)

Столь авторитетный источник, как "Британская энциклопедия", еще более определенно утвержает о том, что пасхальные вычисления окончательно сложились существенно позже IV века н.э. В статье "Никейский собор" сказано буквально следующее: "Собор также пытался установить единые правила даты пасхи, но потерпел неудачу". В статье "Христианство" утверждается: "Первый Никейский собор постановил, что все христиане должны праздновать пасху в один и тот же воскресный день. Однако осталось много расхождений в способах, которые использовались различными церквями для вычисления даты пасхи". Наконец, в статье "Дионисий Малый" говорится: "Дионисий Малый - видный деятель церкви VI века, который считается изобретателем христианского летоисчисления, использование которого распространилось благодаря применению его новых пасхальных таблиц." Таким образом, утверждается, что Никейский собор не сумел выработать конкретных правил определения даты пасхи, а их появление в современном виде связывается с работами Дионисия Малого (VI век).

В заключение этого раздела приведем несколько сокращенный перевод текста Excursus on the subsequent history of the easter question ("Экскурс в последующую историю пасхального вопроса") на сайте Internet Medieval Source Book, в котором излагается история становления вычислений дат пасхи после Никейского собора.

"Различия в методах определения даты пасхи не исчезли после Никейского собора. Александрия и Рим не смогли достичь согласия либо потому, что одна из этих церквей пренебрегала пасхальными вычислениями, либо потому, что другая считала их неточными. Римская церковь продолжала использовать 84-летний цикл, как и прежде - этот факт подтверждается пасхальной таблицей Римской церкви. Этот цикл во многих отношениях отличался от александрийского и не всегда давал одинаковую дату пасхи - фактически римляне использовали совершенно иной метод пасхальных расчетов. В Риме ошибались в определении момента полнолуния, считая его несколько ранее фактического, а в Александрии - несколько позже. [Это легко объясняется разностью широт Рима и Александрии и, как следствие - различным интервалом времени между полнолунием м наблюдением неомении - Ю.К.] Римляне предполагали, что равноденствие происходит 18 марта, в то время как александрийцы считали, что оно случается 21 марта. Наконец, в Риме правила определения пасхи отличались также и от греческих - римляне не праздновали пасху на следующий день, если полнолуние приходилось на субботу.

Уже на следующий год после Никейского собора, т.е. в 326 году, а также в 330, 333, 340, 341, 343 гг., римляне праздновали пасху не в один день с александрийцами. Чтобы положить конец этому несогласию, Сардинский Синод 343 года, как нам известно из недавно открытых праздничных посланий святого Афанасия, вновь поднял вопрос о праздновании пасхи и призвал две стороны (александрийцев и римлян) устанавливать общий день пасхи на протяжении следующих 50 лет путем взаимных консультаций. Этот компромисс через несколько лет перестал соблюдаться. Проблемы, связанные с арианской ересью, и вызванный ими раскол между восточной и западной церквями помешали выполнению сардинского соглашения. Поэтому император Феодосий Великий, после установления согласия в Церкви, счел себя обязанным предпринять новые шаги для достижения полного единообразия в правилх празднования пасхи. В 387 году римляне праздновали пасху 21 марта, а александрийцы - лишь пять недель спустя, т.е. 25 апреля, так как александрийцы считали, что равноденствие наступает 21 марта. Император Феодосий Великий запросил у епископа Александрийского Феофила объяснение такого расхождения. Епископ ответил на пожелание императора и составил хронологическую таблицу пасхальных дат, основанную на принятых александрийской церковью принципах. К несчастью, до нас дошло только введение к этой работе.

Кирилл Александрийский сократил пасхальные таблицы своего дяди Феофила и и определил даты пасхи на предстояшие 95 лет - т.е. с 436 по 531 гг. н.э. Кроме того, Кирилл в письме папе Римскому показал, в чем состояли ошибки в латинских вычислениях; эти доказательства были вновь затронуты в письме протоиерея Александрийского к папе Римскому Льву I. После этого письма папа Лев чаще отдавал предпочтение александрийским вычислениям, а не вычислениям Римской церкви.

Несколько лет спустя, в 457 году, Виктор Аквитанский предпринял усилия по согласованию александрийских и римских пасхальных вычислений. В его таблицах лунных фаз новолуния были более точными, чем в предыдущих таблицах, и основные разногласия между латинскими и греческими вычислениями были устранены; таким образом, римская пасха стала совпадать с александрийской или ненамного отступала от нее. В тех случаях, когда пасхальное полнолуние приходилось на субботу, Виктор не конкретизировал, нужно ли отмечать пасху на следующий день, как делали александрийцы, или отложить ее на неделю. Он указывал в таблицах две даты, предоставляя папе решать, как поступать в каждом конкретном случае. Даже после вычислений Виктора оставались большие разногласия в вопросе об определениии даты пасхи, и они были полностью преодолены лишь Дионисием Малым, который предоставил римлянам пасхальные аблицы, основанные на 19-летнем цикле. Этот цикл полностью соответствовал принятому в Александрии, и таким образом была установлена гармония, которую столь долго и безуспешно пытались найти. Дионисий показал преимущества своих вычислений столь убедительно, что они были приняты в Риме и во всей Италии; однако вся Галлия осталась верна канону Виктора Аквитанского, а в Британии по-прежнему использовался 84-летний цикл, несколько усовершенствованный Сульпицием Севером. Лишь в 729 году большинство церквей Британии перешли на использование 19-летнего цикла. Наконец, при Карле Великом 19-летний цикл окончательно восторжествовал над своими соперниками, и все христиане были объединены."

Григорианская реформа

Как уже отмечалось, ни юлианский календарь, ни метонов цикл, используемые при пасхальных расчетах, не обладают достаточной точностью. Весеннее равноденствие плавно смещается на все более ранние числа марта, а расчетные полнолуния все сильнее запаздывают относительно истинных. Во второй половине XVI века эти расхождения стали весьма существенными. Весеннее равноденствие происходило 10-11 марта, а расчетные полнолуния отставали от реальных на 3-4 дня. Из-за сдвига даты равноденствия пасху часто отмечали не после первого весеннего полнолуния, а лишь после второго, а из-за запаздывания расчетных полнолуний - не в первое, а лишь во второе воскресенье после полнолуния.

В 1582 году при папе Григории XIII была проведена календарная реформа. Цель реформы была изложена в папской булле "Inter gravissimas": "Былo зaбoтoю нaшeю нe тoлькo вoccтaнoвить paвнoдeнcтвиe нa издpeвлe нaзнaчeннoм eмy мecтe, oт кoтopoгo co вpeмeни Hикeйcкoгo coбopa oнo oтcтyпилo нa дecять днeй пpиблизитeльнo, и XIV Лyнe вepнyть ee мecтo, oт кoтopoгo oнa нa чeтыpe и пять днeй oтxoдит, нo и ycтaнoвить тaкжe cпocoб и пpaвилa, кoтopыми бyдeт дocтигнyтo, чтoбы в бyдyщeм paвнoдeнcтвиe и XIV Лyнa co cвoиx мecт никoгдa нe cдвигaлиcь."

Таким образом, календарная реформа - совокупность по крайней мере трех задач. Первая из них - исправить уход даты равноденствия от 21 марта и ликвидировать отклонения расчетных полнолуний от наблюдаемых. Вторая - достичь того, чтобы равноденствие в календаре удерживалось около 21 марта и в дальнейшем. Третья - принять какие-то меры к тому, чтобы расписание полнолуний не "уходило" от полнолуний истинных.

Первая из задач, очевидно - самая простая. Для возвращения равноденствия на 21 марта из счета дней были выброшены 10 суток - за 4-м октября 1582 года последовало сразу 15-е. Расписание полнолуний также было изменено для соответствия с реальными полнолуниями.

Вторая задача состоит в изменении средней длины календарного года с тем, чтобы она была возможно более близка к продолжительности тропического года. Вообще говоря, идея решения этой задачи единственна: если средняя длина календарного года (365.25 суток) больше длины тропического года, то для уменьшения средней длины календарного года нужно уменьшить количество високосных лет в календаре. Однако способов уменьшения количества високосных лет есть несколько. Один из них - время от времени делать промежуток между високосными годами не в 3, а в 4 простых. Этот способ позволяет добиться того, чтобы момент истинного равноденствия отходил от среднего не более чем на полсуток, т.е. действительно зафиксировать равноденствие в пределах суток. Однако такой способ имеет и недостаток - трудность определения того, какой год является високосным. В юлианском календаре этот вопрос сводится к нахождению остатка от деления номера года на 4, а в подобном календаре пришлось бы определять, какой год является високосным, по существенно более сложным правилам.

Авторы реформы поступили иначе - они по сути сохранили юлианский календарь, время от времени вводя в него исправления. Исправления эти вводятся только в вековые годы (годы, номера которых кратны 100). Вековые годы, номера которых не кратны 400, считаются не високосными, а простыми. Таким образом, исправления проводятся три раза в 400 лет, а средняя длина года в новом календаре - 365.2425 суток, что гораздо ближе к среднему промежутку времени между весенними равноденствиями, чем средняя длина года юлианского календаря (365.25 суток). Такое решение привело к тому, что весеннее равноденствие в григорианском календаре приходится на моменты от 15 часов 4 минут 19 марта (в 1696 году) до 19 часов 16 минут 21 марта (в 1903 году) - т.е. интервал моментов равноденствия составляет несколько более двух суток. Столь большой интервал - более чем вдвое больший, чем тот, которого можно достичь при оптимальном распределении високосных годов - плата за простое правило високосов. В целом же григорианский календарь, по замечанию американского астронома Г.Мойера, "представляет собой весьма удовлетворительный компромисс между высокой точностью и крайне желательной простотой" [1].

На рисунке 5 приведен график моментов весеннего равноденствия в григорианском календаре с 1600 по 2200 годы. Из графика видно, что на протяжении века (или двух подряд - XX и XXI) календарь ведет себя как юлианский - моменты равноденствия плавно смещаются на более раннее время. Три раза за 400 лет проводится коррекция, и момент равноденствия скачком отодвигается позже на сутки (из-за пропуска високосного года).

Рисунок 5. Моменты весеннего равноденствия в григорианском календаре в 1600-2200 гг.н.э.

Теперь рассмотрим, как была решена последняя задача - ликвидация нарастающего со временем рассогласования "дня 14-й Луны" и расчетной даты пасхального полнолуния. Использованное решение - достаточно простое и остроумное. В новом алгоритме расчета даты пасхи используется все тот же 19-летний цикл и расписание полнолуний. Для устранения векового смещения дат полнолуний используются две поправки. Первая из них - "солнечная" - компенсирует влияние коррекций календаря. Например, 1700 год - простой, хотя в юлианском календаре он был бы високосным. "Солнечная" поправка сдвигает расписание полнолуний в те вековые годы, которые не являются в григорианском календаре високосными, на сутки позже. (Сдвиг дат, разумеется, циклический - если в результате получается дата позже 19 апреля, то берется дата на 30 дней ранее). Таким образом, "солнечная" поправка восстанавливает метонов цикл юлианского календаря, обеспечивая те же самые расчетные даты полнолуний, которые получились бы при использовании старого алгоритма их расчета (разумеется, с другим начальным расписанием полнолуний, соответствующим концу XVI века - времени проведения реформы). Авторам реформы было хорошо известно, что метонов цикл в юлианском календаре смещается на сутки относительно истинных фаз Луны за 300 с небольшим лет. Для компенсации этого эффекта ими была введена вторая поправка - "лунная". Она сдвигает расписание полнолуний на сутки 8 раз за 2500 лет. Коррекция также проводится только в вековые годы - семь раз через 300 лет, а восьмой - через 400, а в среднем - через 312.5 лет, что очень хорошо компенсирует вековой сдвиг метонова цикла.

Метод решения задачи о компенсации векового сдвига полнолуний в григорианском календаре несколько напоминает старую шутку об одном математике, которого попросили вскипятить воду: "Выльем воду из котла, вытащим дрова из печки и сведем задачу к предыдущей - ее решение уже известно". "Солнечная" поправка восстанавливает метонов цикл юлианского календаря, сдвигая расписание полнолуний на сутки в те годы, которые не являются високосными в григорианском календаре, но были бы таковыми в юлианском - таким образом, задача действительно сводится к предыдущей. "Лунная" же поправка компенсирует вековой уход исходного метонова цикла.

На рисунке 6 показан возраст Луны на 18 часов вечера расчетного пасхального полнолуния, вычисляемого по григорианскому алгоритму.

Рисунок 6. Истинный возраст Луны на 18 часов в григорианское расчетное пасхальное полнолуние (по мировому времени) в 1600-5000 гг.н.э

На графике четко видно, когда осуществляется "лунная" поправка - расписание полнолуний скачком смещается на сутки в 1800, 2100, 2400 гг. и так далее через 300 лет до 3900 года, после которого между коррекциями проходит 400 лет до следующей коррекции в 4300 году. Видно также, что в подавляющем большинстве случаев возраст Луны составляет от 14 до 16 суток, т.е. расчетное полнолуние либо совпадает с "днем 14-й Луны", либо запаздывает на сутки. Более наглядно эти данные представлены в таблице 3.

Таблица 3. Близость расчетных григорианских полнолуний и наблюдаемых "дней 14-й Луны" в 1600-5000 гг.

Расчетное полнолуние:Случаев %Опережает на двое суток6 0.18Опережает на сутки365 10.73Совпадает1797 52.84Отстает на сутки1169 34.37Отстает на двое суток64 1.88

Итак, расчетные полнолуния совпадают с наблюдаемыми более чем в половине случаев, более чем в трети - отстают на сутки и опережают на сутки примерно в одном случае из десяти. Доля расхождений на двое суток весьма мала (около двух процентов). Собственно говоря, трудно достичь существенно лучшей точности при использовании столь неточного метода, как 19-летний метонов цикл.

В заключение этого раздела приведем два алгоритма расчета даты григорианской пасхи. Как и ранее, все деления в них - целочисленные, а знаком процента обозначается нахождение остатка.

Первый из алгоритмов выглядит следующим образом:

G = year % 19;
C = year/100;
H = (C - C/4 - (8*C+13)/25 + 19*G + 15) % 30;
I = H - (H/28)*(1 - (H/28)*(29/(H + 1))*((21 - G)/11));
J = (year + year/4 + I + 2 - C + C/4) % 7;
L = I - J;
month = 3 + (L + 40)/44;
day = L + 28 - 31*(month/4);

В этом алгоритме G - это уменьшенное на единицу золотое число, I - число дней от 21 марта до расчетного пасхального полнолуния, J - день недели, на который приходится пасхальное полнолуние. В третьей строке алгоритма легко обнаруживаются "солнечная" и "лунная" поправки: первая из них - это выражение C-C/4, а вторая - (8*C+13)/25, где C - частное от целочисленного деления номера года на 100, полученное в предыдущей строке.

Второй алгоритм приведен в [2]. В нем не вычисляется в явном виде смещение даты пасхального полнолуния от 21 марта. Его анализ предоставляется читателю в качестве упражнения.

a = year % 19;
b = year / 100;
c = year % 100;
d = b / 4;
e = b % 4;
f = ( b + 8 ) / 25;
g = ( b - f + 1 ) / 3;
h = ( 19 * a + b - d - g + 15 ) % 30;
i = c / 4;
k = c % 4;
l = ( 32 + 2 * e + 2 * i - h - k ) % 7;
m = ( a + 11 * h + 22 * l ) / 451;
n = 3 + ( h + l - 7 * m + 21 ) / 31;
p = ( h + l - 7 * m + 21 ) % 31;
month = n;
day = p + 1;

Насколько точен григорианский календарь?

Чтобы оценить качество проделанной реформаторами календаря работы, исследуем его точность.

В большинстве работ такой анализ выглядит примерно так: истинная продолжительность тропического года составляет 365.2422 суток, а средняя продолжительность года григорианского календаря - 365.2425 суток. За год разница составит 0.0003 суток, а разница в целые сутки накопится за 1/0.0003 лет, т.е. примерно за 3300.

В этих рассуждениях, однако, не учитываются два существенных обстоятельства. Во-первых, длина тропического года, выраженная в сутках, несколько уменьшается. Это вызвано уменьшением скорости вращения Земли - строго говоря, не год сокращается, а сутки удлинняются, и в году их помещается все меньше и меньше. В таблице 4, заимствованной из [1], показано уменьшение длительности тропического года.

Таблица 4. Изменение длины тропического года.

ГодДлина года-3000365.242500 0365.242316 1900365.242199 4000365.242070

Отсюда следует, что разность между длиной тропического года и средней длиной года в григорианском календаре увеличивается со временем - сейчас она действительно составляет около 0.0003 суток, но через 2000 лет она увеличится до 0.00043 суток. Следовательно, смещение дат равноденствия в григорианском календаре будет происходить с увеличивающейся скоростью, и ошибка в су